The ODE45 Function
To numerically solve ODE's in Matlab, use the Matlab ode45 function.
The ode45 command is a variable step solver (which means that it automatically
chooses the value of h for each time step) and is based on an explicit Runge-Kutta (4,5) formula,
the Dormand-Prince pair. This is a combination 4th and 5th order method and thus it is very accurate.
The ode45 function needs only the solution at the immediately preceding
time point to compute the next value of y(tk). Thus it has the same character as the
simple Euler's method that we studied earlier. It is beyond the scope of this course to
discuss these higher order methods, but if you are interested, a reference for this
method is Dormand, J. R. and P. J. Prince, "A family of embedded Runge-Kutta formulae",
J. Comp. Appl. Math., Vol. 6, 1980, pp 19-26.
Solving an ODE using Matlab's ode45
Recall that numeric solutions to ODE's create sets of points and require an ODE in general form and an initial condition. For Matlab to solve ODE's, these steps must occur.
- The ODE must be written in standard form. This means that the derivative is on the left hand side of the equal sign and the calculation of the derivative is on the right hand side of the equation.
- A function must be defined that evaluates the right hand side of the ODE and
follows a specific form as required by
ode45. This form is described next. - An initial condition (ie. y(0)=10) must be known.
- The
ode45function must be called with an appropriate time span and initial condition. - The results of
ode45are then plotted to show the solution.
The rhsode function. This function can have any valid function name,
but it must be defined as follows for it to work properly when called by ode45.
The Matlab code for numerically solving an ODE with initial condtion y(0)=10, is:
1 clear 2 tspan = [ 0, 8 ]; % set time interval from t=0 to t=8 3 y0 = 10; % set initial condition, y(0)=10 in this case 4 % rhsode is a user-defined function that evaluates the r.h.s. of the ode 5 [t,y] = ode45( @rhsode , tspan , y0 ); 6 plot(t,y) % plot the solution returned by ode45 7 [t,y] % print out t and y(t)
Type or copy the above code into a Matlab m-file named solveode.m.
The line numbers are only for reference and are not part of the script.
Here is a line by line description of the code:
Line 1 clears out all previously defined variables. This is important to do, because Matlab remembers the values of variables from previously executed scripts and these can foul-up a calculation.
Line 2 sets the initial time and the ending time at which the solution is computed.
These two numbers are assigned to the row vector called tspan.
This variable name could be anything, but tspan is somewhat descriptive of its contents.
Notice that this line does not use a colon (:) to generate a list of numbers --
tspan is a vector containing only two elements, the start time and the end time.
Line 3 assigns the initial value of the unknown solution function, as y0=10.
We give the initial value the name y0.
From tspan we know that the initial value of t is 0.
Thus lines 2 and 3 together specify the complete initial condition y(0)=10
and the ending time of the solution function, t=8.
Line 4 is a comment that describes the next statement.
Line 5 is the call to the Matlab ode45 command.
The syntax of line 5 is very important to understand.
The left hand side of the line 5 assignment statement names two vectors that will be
assigned the values that the ode45 function returns.
- The
tvector variable will be assigned the times tk at which the ODE solution was computed byode45. - The
yvector variable will contain the result of the solution function yk for each corresponding time tk.
The right hand side of the line 5 assignment statement calls the ode45 function.
- The first argument,
@rhsodeis a function handle for a Matlab function that evaluates the right hand side of an ODE. This function, whatever its name, must be defined to compute the value of the right hand side of the ODE when the ODE is written in standard form. - The next argument is the
tspanvariable that was defined to specify the beginning and ending of the time over which the calculation is to be done. - The final argument is the
y0variable specifying the initial value of the solution functiony(t).
Thus the pair of vectors [t,y] comprise the numerical solution of the ODE
defined by the rhsode function since they define points on a graph that can be plotted.
The vectors may be hundreds of elements long and will always have the same number of elements.
Remember that vector indexing starts with 1 rather than 0, and that the initial time
t0 and initial value y0 are stored in vector elements
t(1) and y(1), respectively.
This can be especially confusing when your initial time t0 is zero.
Line 6 plots the solution t vs. y.
Recall that these are both vectors so that the plot command plots all of these points on a graph.
Because ode45 chooses h to be very small, there are enough solution points
so that the plotted curve looks continuous. However, it is really just a sequence of discrete points.
Line 7 outputs the contents of t and y. This line is not necessary and
is usually not done. We show it here so that students can see that the step size between
successive points in time t is not uniform. The particular size of the time step
is a property of the specific Runge-Kutta algorithm chosen.
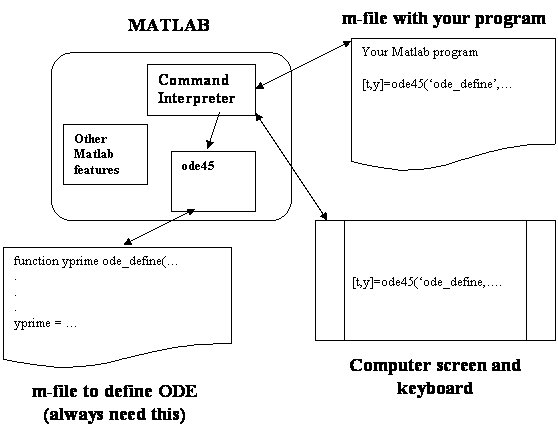
This diagram shows how Matlab works to numerically solve an ODE system.
The main script sets up the call to ode45.
The Command Interpreter interprets the call and executes the
the ode45 function's code. The code in the ode45
function uses the current t and y(t) values to pick the next time value
and y(t) estimate. It then calculates the derivative, stores it, and uses it
to calculate the next values. This continues until the end time is reached
and the results are returned to the caller.